Diz a lenda que a Amazon usa problemas complicados em seu processo seletivo. O que um destes problemas nos ensina?

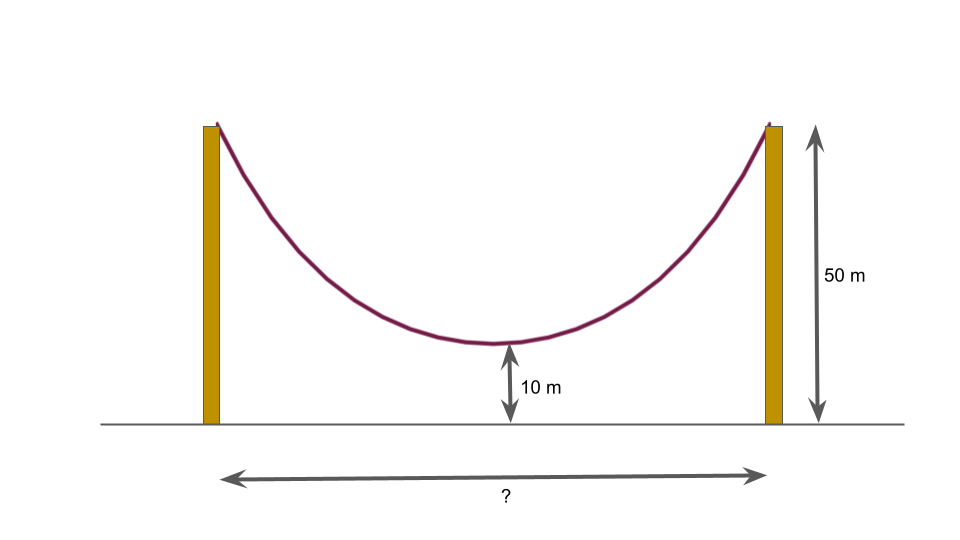
Não pare de ler se você tem alergia a matemática, por favor.

A corda vai descrever uma curva entre os dois postes. Você pode pensar que a corda descreve uma parábola, e estaria na nobre companhia de Galileu Galilei, que formulou esta hipótese. No século 17, cientistas como Bernoulli, Leibniz e Huygens demonstraram a solução correta da equação que descreve a forma de uma corda ou corrente pendurada entre dois pontos. O nome desta forma é Catenária, e é utilizada também na arquitetura, invertida, em arcos com a melhor resistência por quantidade de material.

A equação da Catenária é dada por y = a (cosh (x/a)).

Sim, cosseno hiperbólico, que você nem lembrava que existia… E o parâmetro “a” é a relação entre a tensão horizontal e o peso por unidade de comprimento da corda ou corrente, portanto uma propriedade do material que não é informada no problema e que altera o formato da catenária. Uma corda fina e uma corrente pesada descreverão curvas diferentes. Será que os candidatos a uma vaga na Amazon deveriam conhecer esta equação e estimar o parâmetro “a” ?

A primeira chave é que a figura nos faz pensar que o problema é um caso típico da solução de uma equação. Mas observe que as medidas não descrevem a real proporção do problema proposto: o desenho não está na escala correta e ele nos induz a erro. No desenho, a corda é muito mais longa do que 80 m e o ponto mais baixo está muito mais distante do solo do que 10 m, tomando como referência a escala dos postes.

Refletindo um pouco mais, encontramos a outra chave: será que o problema proposto poderia ser um caso especial em que cossenos hiperbólicos e propriedades da corda fossem irrelevantes? 

O ponto da corda mais próximo ao solo é a metade de seu comprimento, não é? Como a corda mede 80 m, este ponto estará a 40 m das extremidades. Se o poste tem 50 m de altura, a única maneira deste ponto estar a 10 m do solo é se a corda for paralela ao poste, e portanto a distância entre os postes for zero ! Os postes estarão colados, e a corda estará dobrada em duas. E é claro, este ponto também é descrito pela equação geral, mas não preciso dela para resolver o problema específico. E você poderia argumentar que a corda pendurada deste jeito não se parece mais com uma Catenária, mas isso também não fazia parte do enunciado do problema…

Claro que há muitas situações em que precisaremos usar o equacionamento geral. Mas sair fazendo contas neste caso particular  vai nos permitir chegar à resposta correta mais rapidamente? Provavelmente este caminho nos levaria a uma longa busca sobre qual parâmetro "a" deveria ser usado.

Eu apresentei este problema ao ChatGPT, e as respostas foram hilárias.

Primeiro, ele aproximou o problema para dois triângulos, fez um erro de cálculo e concluiu que a distância entre os postes era de 67,5 m. Então eu sugeri que a forma da curva não era uma reta, talvez uma parábola? Ele me corrigiu, disse que a forma era de uma catenária e apresentou a equação correta. Mas se confundiu novamente ao fazer os cálculos, arrumou um jeito de sumir com o parâmetro “a” e concluiu que a distância entre os postes seria um pouco maior, “aproximadamente 69,6 m”. Eu questionei o resultado, disse que era possivelmente muito grande para uma corda de apenas 80 m e ele fez uma sugestão brilhante: pendurar a corda a uma altura menor, de tal forma que a distância do solo fosse 10 m ! Não é a solução do problema, mas a ideia entrega uma corda amarrada entre dois postes situada a 10 m do solo...

Tratar um problema complexo como se fosse simples é um grande risco, mas deixar de enxergar a simplicidade de um problema não é um risco menor. O problema proposto por Jeff Bezos é muito mais simples do que o problema que Galileu se propôs a resolver. Saber se você deve pensar um pouco mais, usar o ChatGPT ou contratar um especialista é o comportamento chave, e a Zinneke pode ajudar você. Fale conosco.

___

Eduardo Rocha acredita que a curiosidade, o aprendizado contínuo e a reflexão são motores da criatividade e da inovação. Fundou a Zinneke com o propósito de ajudar empresas a resolver problemas, da forma mais rápida e efetiva. Fale conosco se tem um problema que precisa de ajuda.

Photo by Ricardo Gomez Angel on Unsplash. Thanks !

#inovação #problemas #criatividade