Otimização X otimização matemática: resultados melhores são resultados ótimos?
Sempre se busca melhorar um patamar já atingido. Mas diante de um cenário, é possível determinar quais são os patamares ótimos?
É cada vez mais comum ouvirmos o termo 'otimização' para designar estratégias de melhoria em processos de decisão: “otimizar tempo”, rota, custo, lucro. Entende-se por melhoria uma aproximação de um valor desejado, quando comparada a um valor anterior. Assim, “otimizar o tempo” pode significar prazo menor. “Otimizar a rota”, um trajeto menor ou mais rápido. “Otimizar custo” seria reduzir gastos com o fornecedor ou com os processos. E “otimizar lucro” seria aumentar a margem. Afinal, qualquer melhora obtida já é ótimo, não é mesmo?
Muito bom! Mas ainda não é ótimo.
Na matemática o significado de “otimização” é mais ambicioso do que uma melhoria. É obter o mínimo (ou máximo) possível e não apenas um tanto a menos ou um tanto a mais. A otimização matemática resolve problemas começando pelo modelo matemático específico que descreve a situação na forma de funções e equações matemáticas. Toda a situação e dados do problema são descritos através de três elementos:
- Variáveis de controle - podem variar durante o processo e influenciam direta ou indiretamente o objeto a ser otimizado: tempo parcial, distância local, nº de itens de produção, custo fixo ou variável, demanda, receita entre outros.
- Função objetivo - função das variáveis de controle que mede o objeto a ser otimizado: tempo total, distância total, custo total, lucro total líquido etc.
- Restrições - equações ou inequações matemáticas que impõem limitações às variáveis: disponibilidade ou limitação de tempo, distância, matéria prima disponível e entre outros.
Antes de sair resolvendo, montar o problema.
Além de profunda intimidade com o contexto que os envolve, modelar matematicamente os problemas práticos exige conhecimento técnico na escolha do modelo matemático adequado, sem o qual a solução ótima pode nem ter significado! Aqui, a ajuda de um especialista é valiosa para simplificar e apurar os modelos matemáticos e determinar as fórmulas e equações adequadas ao método de otimização escolhido, que em geral é específico para cada tipo ou classe, seja da função objetivo, seja das equações envolvidas.
Definição
Otimização Matemática ou Programação Matemática é a área da Matemática Aplicada que estuda métodos e algoritmos para resolver problemas tipo: “Dada uma função real, de variáveis reais, determinar os valores das variáveis para os quais a função assuma seu maior valor (máximo) ou o seu menor valor (mínimo), sujeito a eventuais restrições”. São chamados de Problemas de Programação Matemática ou
Problemas de Otimização. A função dada é chamada de
função objetivo. E o seu valor mínimo (ou o máximo) é chamado de
ótimo. O conjunto de valores das variáveis para o qual a função assume o ótimo é chamado de
solução ótima, ou otimizador, e o processo de resolução do problema é chamado de
otimização.
Produção e comercialização: eis um exemplo interessante.
Para determinar a quantidade produzida de modo a maximizar o lucro, os livros de Cálculo e Administração apresentam diversos modelos matemáticos, que consideram a
variável
“total de itens a produzir” (denominada
x) e a
função objetivo: lucro = receita - custo, em função da quantidade de itens produzidos, denotada por L(x). Em modelos mais simples, L(x) pode ser uma função do segundo grau. Em modelos mais complexos, podem ser funções de outras classes. O problema de otimização consiste em determinar
x para que L(x) tenha valor máximo, considerando como restrição que x seja positivo, ou uma limitação da matéria prima disponível.
Encontrar a solução ótima é uma tarefa desafiadora.
Encontrar o valor máximo ou mínimo de um conjunto requer comparar todos os valores, o que pode ser impraticável conforme o conjunto aumenta, mesmo num computador! Por isso os algoritmos e softwares de otimização matemática utilizam estratégias mais sofisticadas do que só investigar os valores. Baseados no estudo das funções e equações envolvidas no modelo, eles utilizam as derivadas para gerar uma sequência de valores convergindo para o ótimo.
Ótimo relativo?
Apesar de eficiente, a estratégia com uso de derivadas pode gerar sequências de valores que convergem para ótimos relativos (também chamados locais), que são máximos ou mínimos apenas em um subconjunto de valores. No gráfico, onde o eixo horizontal são as variáveis e o eixo vertical a função objetivo, vemos os máximos local e global. Por definição, o global é ótimo. Mas ambos podem ser considerados ótimos quando a variável está restrita a um subconjunto de valores (em amarelo no gráfico).
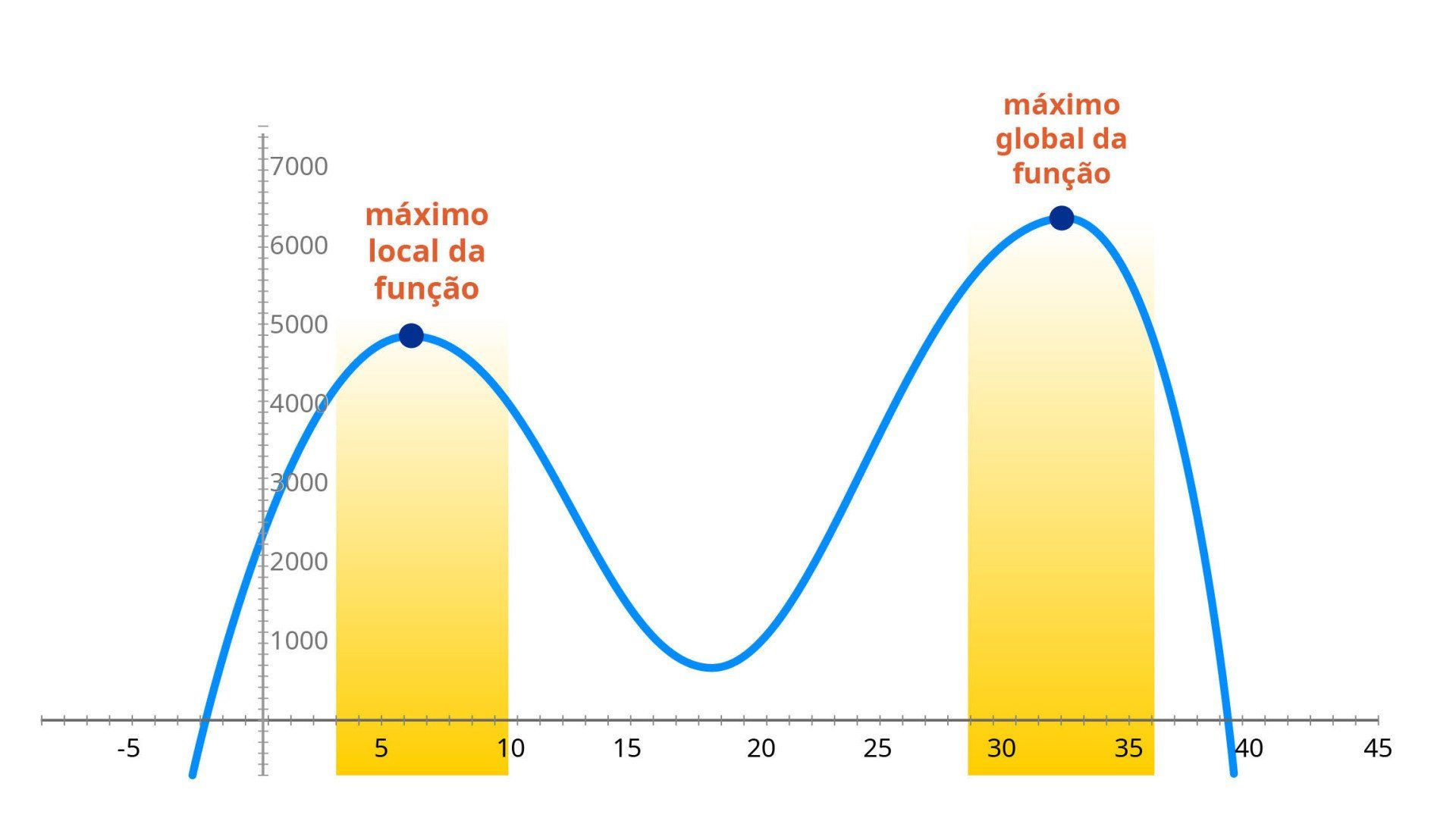
Há casos em que é interessante evitar ótimos locais, como em machine learning e inteligência artificial, escolhendo modelos matemáticos com funções côncavas ou convexas.
Os algoritmos de otimização também podem favorecer e explorar as características das funções e equações, tornando o processo mais eficiente para cada modelo. Existem softwares e algoritmos específicos para modelos lineares, não lineares, quadráticos, com restrições em caixa, estratégias globais (sem usar derivadas) entre outros. A eficiência para resolver problemas de otimização também depende da escolha do método adequado ao modelo matemático.
A otimização matemática é importante não só em problemas diretos mas em situações indiretas, como subrotinas para algoritmos mais gerais, machine learning e inteligência artificial. É uma ferramenta valiosa para dar uma noção de quanto as melhorias realizadas na empresa estão próximas dos parâmetros matematicamente ótimos. É uma área em constante avanço, tanto teórico quanto computacional.
Junto com a Zinneke, a SuM Analytics se propõe a estudar problemas, propor modelos e soluções utilizando ferramentas matemáticas, buscando um novo patamar de qualidade na tomada de decisões.
---
Suzana Castro, sócia da SuM Analytics, é pesquisadora, docente em Matemática. Tem interesse em atividades que promovam o conhecimento da matemática de modo amplo, aplicado e motivador.
Marcelo Meneghetti, sócio da SuM Analytics, é publicitário, psicanalista, docente em comunicação, apaixonado pela mente humana, motivação, paradoxos e inovação.
#otimização #otimizaçãomatemática #maximizar #minimizar










